37803
%7B%22isLastPage%22%3Afalse%2C%22notes%22%3A%5B%5D%2C%22pid%22%3A%22t37803%22%2C%22tid%22%3A%2237803%22%2C%22mainForumsId%22%3A%5B%22204%22%5D%2C%22categoriesId%22%3A%5Bnull%5D%2C%22tcId%22%3A%5B%5D%7D
%7B%22isEditMode%22%3Afalse%7D
一道初中物理题,求圆满解释
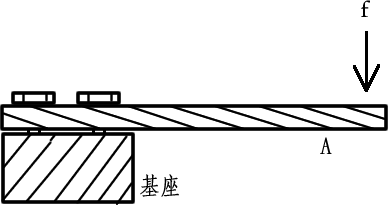
如图,一个轻质、弹性杆A,一端固定在一个足够牢固的基座上。
如果向另一端施加一个力f,这个杆子会产生一个弹性形变(向下弯曲,比如弯曲2mm)。
![A.gif]()
用螺栓在A杆一端连接一根加长杆B,B的特点是轻质,且刚性,B的长度和A相同。
如果给B杆的另一端施加相同的力f,请问A杆的型变量是多少?
![B.gif]()
如果在A杆一端连接B杆时,方向与A杆相反,只不过为了避免两个杆子帖在一起,在中间垫有刚性轻质物体C。在B杆一端也施加力f,请问A杆型变量是多少?
![C.gif]()
忽略A杆螺栓处的局部变形。
如果向另一端施加一个力f,这个杆子会产生一个弹性形变(向下弯曲,比如弯曲2mm)。
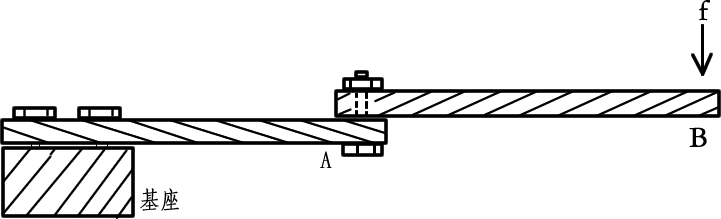
用螺栓在A杆一端连接一根加长杆B,B的特点是轻质,且刚性,B的长度和A相同。
如果给B杆的另一端施加相同的力f,请问A杆的型变量是多少?
如果在A杆一端连接B杆时,方向与A杆相反,只不过为了避免两个杆子帖在一起,在中间垫有刚性轻质物体C。在B杆一端也施加力f,请问A杆型变量是多少?
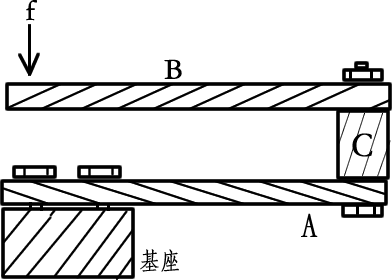
忽略A杆螺栓处的局部变形。
加载全文