心血来潮,决定把上次搞得SVPWM算法的推导过程整理一下,然后.....今天整整一天都在干这个.............. 功夫不负有心人,终于搞出来个不像科普文章也不像论文的怪文........... 各位大神轻点拍砖啊...........
以下由bg8npk搬运
搞SVPWM的目的呢,其实就是想让电机平稳地旋转,这次主要说说三相同步电动机(PMSM)的SVPWM控制吧(三相电机结构还请各位自行google)。
PMSM定子的三个绕组嘛,其实可以看做三个电磁铁,而且它们的方向互相成120°角,而它们产生的磁场强度呢,又是和通过它们的电流成正比的,也就是说,我们可以分别控制三个绕组的电流,来分别控制三个电磁铁的磁场强度,进而在电动机内叠加出一个磁场矢量。
PMSM的转子我们可以看做一个简单的永磁体,而上面那个磁场矢量可以看做另一个磁铁,所以,三相同步电机的原理通俗的讲呢,就是两个条形磁铁摞一块,转动上面那个,下面的也跟着转………
而为了能让电机平稳地转动,我们希望电机的定子磁场矢量能以恒定的速度旋转,并且保持磁场强度大小不变。前面说到,磁场强度是和绕组电流成正比的,所以呢,我们需要一个在空间中匀速旋转并且大小不变的电流矢量(电流矢量是个比较抽象的概念,其实它是由三相绕组的三个电流叠加起来的,稍后会详解)。 假设某一时刻,这个电流矢量是这么个情况:
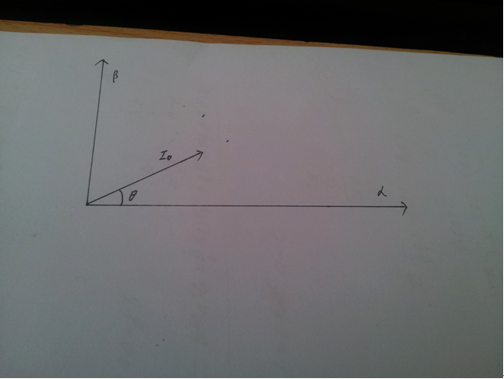
其中坐标系中α轴与电机的A相绕组的方向一致,β轴与α轴成90°角
那么经过一段很小的时间△t之后,这个电流矢量又旋转了一点点:
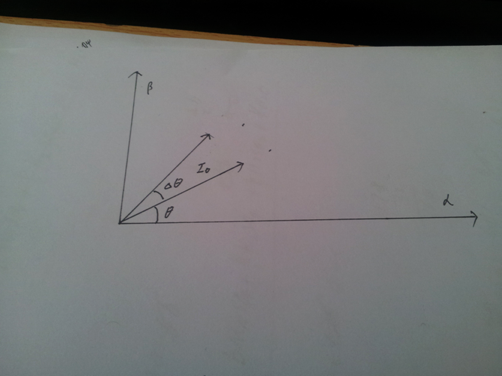
由向量的加法运算可知,为了让电流矢量实现这个旋转,我们需要在这个△t中给它施加一个△I:
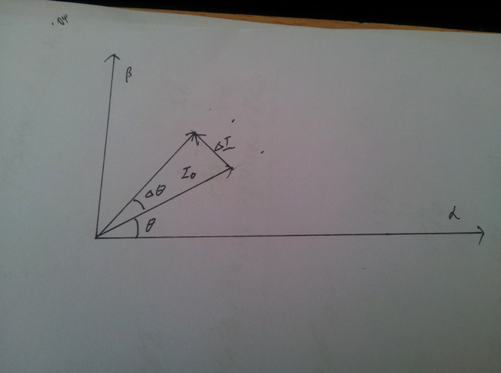
如果我们忽略电动机绕组的内阻的话,电动机其实可以近似为一个感性的负载,那么对于一个电感,如果给它加上恒定的电压,他的电流会随着时间线性增长,所以,为了能给电动机施加这个△I,我们只需要用一个和△I方向相同的电压矢量,再作用△t的时间,就OK啦。
恩,接下来的一个△t也是差不多这么个情况,有点不同的是△I的方向也转了一点点。随着一个一个△t转下去,电流矢量会转上一整圈,然后△I也就会转上一整圈。当我们把△t取的足够小的时候,三角形I也就进化成为一个在空间中匀速旋转的矢量。
由此可见,我们只要给PMSM施加一个大小不变,匀速旋转的电压矢量,就可以在PMSM内部形成一个大小不变,匀速旋转的电流矢量,继而再形成一个大小不变,匀速旋转的磁场矢量*(相信很多人已经有点晕了……其实我也晕……..)*
接下来的问题就是………怎么通过控制三相绕组上的电压,才能叠加出我们想要的电压矢量呢?
首先呢,先来一张三相全桥的电路图:

恩,如果我们让一个桥臂输出高压,另两个桥臂输出0,那么我们可以得到三个互成120°角的电压矢量:

如果让两个桥臂输出高压,另一个输出0,那么我们又可以得到三个电压矢量,相当于两个基本电压矢量的叠加:

如果三个桥臂同时输出0或高压,PMSM的相电压为0,所以我们又得到两个零矢量。 可以看出,除了两个零向量外的六个矢量把整个平面分成了6个扇区,在任意时刻,旋转的电压矢量肯定会落在某一个扇区里。我们给这几个扇区编一下号:

其中U0 U2 U4这三个向量称为主向量,U1,U3,U5称为辅向量。易知U0-U5的幅度都相同,均为三相全桥的直流供电电压,设这个电压为Udc。
SVPWM的基本实现方法呢,**就是在一个PWM周期内。调节一个扇区两边的两个电压矢量和两个零矢量的作用时间,根据平均值等效原理,来合成出我们想要的电压矢量。**假设我们想要的电压矢量正好落在第一扇区里面,那么大致情况就是这样滴:

恩,设一个PWM周期为T,主向量U0作用时间为T1,辅向量U1作用时间为T2,零向量作用时间为T0,那么有T=T0+T1+T2
由向量的叠加与分解可知,我们要输出的Uout在两个坐标轴上的分量分别等于主向量辅向量经过平均值等效后的两个向量在两个坐标轴上的分量之和……好吧我承认我语文不好……..
那么就有如下关系
Uout * COSθ =(T1/T)Udc+(T2/T)Udc * COS 60°
Uout * SINθ =(T2/T)Udc * SIN 60°
T0 = T-T1-T2
令Uα=Uout * COSθ Uβ=Uout * SINθ
解得
T0=(1-Uα/Udc -Uβ/√3*Udc)T
T1=(Uα/Udc – Uβ/√3*Udc)T
T2=2UβT/√3*Udc
再令X=UαT/Udc Y=UβT/√3*Udc
就有
T0=T-X-Y
T1=X-Y
T2=2*Y
设A B C三相全桥三个桥臂的占空比分别为D1 D2 D3,那么输出U1只需要A相桥臂输出高压其他两个桥臂输出0就行,U2需要A B两个桥臂输出高压,C相输出0,零向量可以让三个桥臂同时输出高压或0,一般情况下我们让两个零向量的作用时间相同,那么就有
D1=(T0/2 + T1 + T2)/T=(1+X+Y)/2
D2=(T0/2 + T2)/T=(1-X+3Y)/2
D3=T0/2*T=(1-X-Y)/2
恩,第一个扇区的推导就是这样,后面的五个扇区的推导过程类似,实在不想挨个把五个扇区的详细推导都打上来了…….太多了,接下来就把结果写上来吧
第二个扇区:
D1=1/2 +X
D2=1/2 +Y
D3=1/2 –Y
第三个扇区
D1=(1+X-Y)/2
D2=(1-X+Y)/2
D3=(1-X-3*Y)/2
第四个扇区
D1=(1+X+Y)/2
D2= (1-X+3Y)/2
D3=(1-X-Y)/2
第五个扇区:
D1=1/2 +X
D2=1/2 +Y
D3=1/2 –Y
第六个扇区
D1=(1+X-Y)/2
D2=(1-X+Y)/2
D3=(1-X-3*Y)/2
其实我们可以发现,第一第四扇区、第二第五扇区还有第三第六扇区的占空比都是相同的,有了这些占空比,我们就可以很方便的写出SVPWM程序了
最后附上C演示程序
<code class="language-c">#include <stdio.h>
#include <math.h>
#define PI 3.141592653
#define SQRT_3 1.732051
#define DEPTH 256 /*数据深度,即存储单元的个数*/
#define WIDTH 8 /*存储单元的宽度*/
void svpwm(void);
unsigned int Sampling = 256;
unsigned char CCR1, CCR2, CCR3;
double x,y;
double PI2;
double cosa;
double buffer[6];
double Vdc = 100;
double Vo = SQRT_3*Vdc/2;
int i;
int s1,s2,s3,s4,s5;
void init(void)
{
PI2 = PI * 2 / Sampling;
s1 = Sampling/6;
s2 = Sampling/3;
s3 = Sampling/2;
s4 = 2*Sampling/3;
s5 = 5*Sampling/6;
cosa = 2*cos(PI2);
buffer[0] = -sin(PI2) *(Vo / Vdc) /(2* SQRT_3);
buffer[1] = 0;
buffer[2] = 0;
buffer[3] = cos(PI2) * (Vo / Vdc)/2;
buffer[4] = Vo / (Vdc*2);
buffer[5] = Vo / (Vdc*2);
}
int main(void)
{
init( );
for (i = 0; i < Sampling; i++)
{
svpwm( );
printf("%d %d %d %d \n", i,CCR1,CCR2,CCR3);
}
}
while(1);
}
void svpwm(void)
{
x = buffer[5];
y = buffer[2];
buffer[2] = cosa * buffer[1] - buffer[0];
buffer[5] = cosa * buffer[4] - buffer[3];
buffer[0] = buffer[1];
buffer[1] = buffer[2];
buffer[3] = buffer[4];
buffer[4] = buffer[5];
if (i <= s1) 判断扇区,计算占空比 { ccr1="(0.5" + x y)*256+256; ccr2="(0.5" - 3*y)*256+256; ccr3="(0.5" } else if (i <="s2)" 2*x)*256+256; 2*y)*256+256; code></=></math.h></stdio.h></code>
[修改于 8年5个月前 - 2016/07/07 17:39:11]
200字以内,仅用于支线交流,主线讨论请采用回复功能。
用霍尔传感器做电流闭环,VVVF给出频率和电流的参考值,估计就能当伺服用了
200字以内,仅用于支线交流,主线讨论请采用回复功能。
warmonkey 发表于 2014-4-27 10:45
只能加100了,楼主好样的
用霍尔传感器做电流闭环,VVVF给出频率和电流的参考值,估计就能当伺服用了
惊现猴子大神......我也正在打算假期搞个伺服系统玩玩
200字以内,仅用于支线交流,主线讨论请采用回复功能。
200字以内,仅用于支线交流,主线讨论请采用回复功能。
D1=(T0/2 + T1 + T2)/T=(1+X+Y)/2
D2=(T0/2 + T2)/T=(1-X+3Y)/2
D3=T0/2*T=(1-X-Y)/2
这几步推倒不太明白,能否详解,十分感谢!
200字以内,仅用于支线交流,主线讨论请采用回复功能。