初涉SDR，感觉这次跨越难度比我从单管机到超外差的跨越还大，概念众多，一时难以消化。

*************************************************************************************

这是我当前学习的的相关知识点

*************************************************************************************

这是常见的几种SDR接收架构，直采，直接转换，超外差，其中

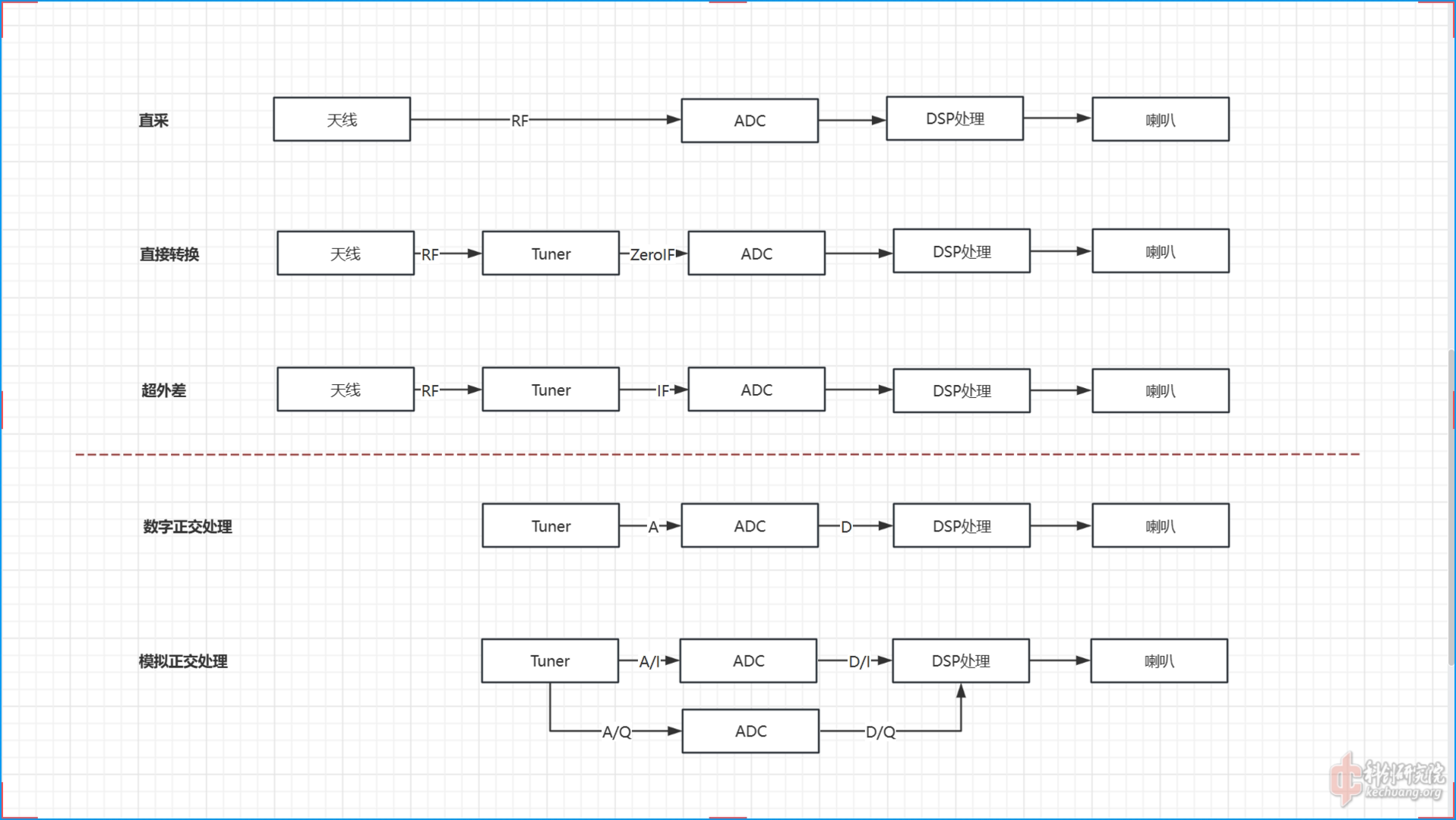
直采-号称是SDR的"圣杯",这种结构把大部分处理过程都移到了数字部分，灵活性极大，但是缺点是依赖一个高速ADC，高速ADC采样的数据又依赖高速DSP处理器，但是高速ADC，高速DSP也就意味着高价格，高成本

直接转换-也交零中频，优点是滤波结构简单，但是存在直流偏差

超外差-也叫低中频，这种结合传统超外差变频和数字处理的优势，是一种低成本方案

在上面的结构中，adc接收到的数据也分为单路模拟信号和双路正交模拟信号，

单路模拟信号优点是只需要一片adc，但是adc采样率要求稍高，正交变换通过数字处理实现，IQ

信号无相位偏差，对dsp性能要求较高

双路正交模拟信号需要两片adc，但是adc采样率要求降低一半，dsp无需做正交变换处理，dsp压力较小，但是IQ信号存在相位偏差

*************************************************************************************

IQ信号，这是一个在数字通讯中非常基本的概念，我在尝试理解这个概念上花费了大量精力，但是感觉还是尚未完全理解，打开教材和网站，对于IQ信号的解释大多是长篇数学推导，以至于都误以为是进入了数学领域，忘记了自己的初衷。我尝试不用复杂难懂的高数，只依赖初等数学来理解和解释这个概念。

*************************************************************************************

这是一个基本的正弦信号曲线，描述一个信号有三大要素，幅度A，频率F，相位P，调制和解调信号也是对这三个属性进行控制和解析，但是这和IQ有什么关系呢？

假如我们在现实世界里面搜集测量一个电波信号，在某一时刻我们获得一个电压值，由于这个电压值是孤立的，可能属于这个正弦波上的任意一点，得到这个点的数值，我们无法确定或者推算出这个正弦波的幅度，频率和相位信息，也就是说当前是信息缺失的，不完整的，你也能会说我们可以等搜集到完整的信号后再去计算，我们这是一个连续的规则信号，如果信号是一个不规则，任意形状的波形，我们处理起来更棘手。

*************************************************************************************

我们举个生活中的列子，现在有一个飘再空中的气球，单凭这一张照片，我们无法判断出气球当前是静止的还是运动的，运动方向是什么，运动速度是多少，当前我们的信息是缺失的，如果再有一张不同时刻的照片我们判断起来就容易多了。

*************************************************************************************

继续回到我们的正弦波，如果我们需要两个点来记录这个波形，哪两个最近点最能表达完整的信息呢，很明显是1/4周期的两个点是包含波形完整信息的最近的两个点，1/2周期和整个周期的两个点因为同在0电位，反而不容易判断，实际上1/4周期的点，可以计算出幅度，频率，相位，而这个属性恰恰是描述一个波最重要的三个要素。

*************************************************************************************

说了这么多，这又和IQ什么关系呢，对于接收来讲IQ信号是对同一个电磁波在1/4周期时刻采集的两个值，接收方要想精确获取此两个周期的值需要PLL做同频同相处理，也就是相干解调的条件，如果不同频同相，此两个数值可能有所偏差。

对于单个波形来讲，是无所谓正弦波和余弦波的，因为你在接收时无法确定相位，正弦和余弦是一个相对的概念，如果我们有两个波形，可以把一个当作参考，把一个当作正弦，另外一个当作余弦来处理。

*************************************************************************************

对于信号合成来讲，如果选择两个同频相位不同的信号来进行合成，也是相差90度相交的最方便合成，

*************************************************************************************

相差180度是两个相反的波形，只会相互抵消消弱，无法影响相位，

*************************************************************************************

360度的就又回到了原点，无法实现更多的变换。

*************************************************************************************

如果合成信号的相位是随机的，那么两个信号合成后会生成两个频率，一个是频率和，一个频率差，如果正交合成可以抵消掉其中一个，只生成一个频率。

*************************************************************************************

以上是项目依赖

********************************************************************************************

am调制

这是am调制公式以及代码

公式说明：

AM：调制结果

A：幅度

Ma：调制指数

Wm：调制信号

Wc：载波信号

t：时间序列

函数参数说明：

FS：采样率

Fm：调制信号频率

Fc：载波信号频率

T：调制时长

m：调制指数

*************************************************************************************

这是am调制测试代码

*************************************************************************************

这是am调制结果图表

********************************************************************************************

这是am解调公式以及代码

公式说明：

I，Q：iq信号

A0：直流信号

m(n):解调信号

函数参数说明：

data：复数信号序列

********************************************************************************************

fm调制

这是fm调制公式以及代码

公式说明：

FM：调制结果

A：幅度

Wc：载波信号

Ma：调制指数

Wm：调制信号

t：时间序列

函数参数说明：

FS：采样率

Fm：调制信号频率

Fc：载波信号频率

T：调制时长

m：调制指数

*************************************************************************************

这是fm调制测试代码

*************************************************************************************

这是fm调制结果图表

*************************************************************************************

这是fm解调公式以及代码

公式说明：

f(n):瞬时频率

I:当前I信号

Ip：前一个I信号

Q:当前Q信号

Qp：前一个Q信号

函数参数说明：

data：复数信号序列

这是一个鉴频器解调算法

*************************************************************************************

原理是通过对两组IQ值计算相位差或者斜率来获得瞬时频率，相位差正比于频率，这是一种比较巧妙的算法

********************************************************************************************

频率偏移

频率偏移，由于我们关心的信号不一定在中心点，因此需要把信号偏移到中心点，要理解这个变换，需要了解欧拉公式，一个上帝公式，e，pi，i，1每一个都是在数学史上里程碑式的存在，以这种方式完美的结合在了一起，我目前还尚未理解这个公式，但是可以把这个公式的作用看作是乘以一个cos函数

*************************************************************************************

这是np.exp(1j*Wc*t)=cos(Wc*t)的测试代码

*************************************************************************************

这是我以两种方式数据生成的图表

*************************************************************************************

这是频率偏移测试代码

*************************************************************************************

这是频率偏移测试图表

********************************************************************************************

重采样

重采样，作用是升高或降低采样率以进行采样率匹配，这里用了up和down两个参数，是为了尽量避免小数形式重采样

*************************************************************************************

这是重采样测试代码

*************************************************************************************

这是重采样对比结果图

********************************************************************************************

滤波

这是滤波代码

函数说明：

数字去加重滤波器，衰减高频作用

data：解码数据序列

bw：带宽

*************************************************************************************

这是滤波对比结果图表

********************************************************************************************

前面的准备工作做好了，我们来实际检验一下我们的工作，先打开sdrsharp来录制一些iq数据

*************************************************************************************

录制的IQ文件在sdrsharp根目录

*************************************************************************************

测试前先看下频率中心点以及采样率

*************************************************************************************

可以看出频率中心点在540K左右，采样率是2M

*************************************************************************************

这是执行偏移之后的结果图，可以看到原来中心点在540k的频率信号现在偏移到了0中心点

*************************************************************************************

执行完代码，文件存放到了wav-files目录

*************************************************************************************

打开wav文件试听一下

*************************************************************************************

我们用同样的方式测试一下am的解调效果，这里我是用的网上下载的一个国外航空管制录制的IQ文件

*************************************************************************************

打开am.wav文件试听一下

********************************************************************************************

项目代码：

python-sdr.zip 162.67MB ZIP 73次下载

频文件：

Python-SDR.mp4 点击下载 ‎

********************************************************************************************

视频地址：XXXXXXXXXXXXXXXXXXXXXXXX/video/BV1e841127CX

项目地址：XXXXXXXXXXXXXXXXX/zhuxianguo/python-sdr