• 表格法求光谱项的原理
• 代码的思路
• 参考文献

本文原地址：东方红茶馆-求解电子光谱项的程序
与原文可能略有不同。

该程序可以处理几乎所有的电子组态（包含的轨道有$s,p,d,f,g$），如 $(\mathrm{s}{)}^1(\mathrm{p}{)}^2(\mathrm{d}{)}^2$这样的组态。但目前不能求解如 $(2\mathrm{p}{)}^2(3\mathrm{p}{)}^2$这一类组态的光谱项。

求原子光谱项有很多种方法，这里只介绍一种思路简单粗暴的方法。某种程度上可称为是逐一枚举的方法。（等你看完说不定会觉得这个方法很low23333）

其实该方法也可看作是结构化学教科书上讲解两个同科电子组态（$(n\text{p}{)}^2$）的光谱项的方法的推广。

表格法求光谱项的原理

我们知道，对于多电子原子中的任意一个电子，其状态可由其单电子原子轨道（波函数）近似描述，其中单电子波函数含有四个量子数。也就是说只要确定了这四个量子数，便能够确定其状态。而组态只能确定电子的主量子数 $n$和角量子数 $l$，并没有进一步描述电子的磁量子数 $m$和自旋磁量子数 $m_s$。

组态的能级分裂就是因为电子的磁量子数和自旋磁量子数的不同，虽然对于多电子原子来说使用总角量子数 $L$、总自旋量子数 $S$和总量子数 $J$的概念会更合适。

所以该方法的第一步是确定某一组态的所有微观能态。

以 ${\text{d}}^3$组态为例。我们首先要考虑其所有的电子排布方式。由于Pauli原理的限制，电子的状态没有完全相同的。d轨道有10个对应的自旋轨道，所以总的微观状态数为 $\left(\begin{array}{c}10\\ 3\end{array}\right)=120$。

以图所示的状态为例，三个电子的磁量子数分别为2、2、1，所以 $M_L=5$。而总自旋磁量子数 $M_S=1/2$。

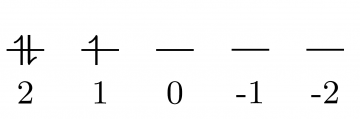
也就是我们要计算一共120种微观能态的 $M_L$和$M_S$。如果手算的话，显然这是一个很麻烦的事情。

当我们将120种组合的 $M_L$和 $M_S$都算出来后，就可绘制出 $M_L$-$M_S$表格。

以总自旋磁量子数为例，三个电子共有四种情况。电子的自旋全部相同以及其中一个电子与另外两个的自旋不同。所以 $M_S=3/2,1/2,-1/2,-3/2$。

相应地，$M_L=5,4,3,\dots ,-4,-5$。我们将各个组合中具有相同 $M_L$、$M_S$分别计数，便可得到该表。

然后只需要一步步从表中提取出光谱项即可。

从最大的 $M_L=5$开始看。$M_L$为 $L$的最大值，$L$的取值范围为 $0,1,\dots ,\pm L$。而且对应的 $S(M_S)=1/2,-1/2$。由此我们可推断出该组态有一 ${}^2\text{H}$的光谱项。

然后我们将表格中二三列的数字均减去1，将该光谱项移除，得到第二步的表。

下图右边的是第二次约去光谱项后得到的表，此时 $L=3\dots -3$，而 $S=3/2,1/2,-1/2,-3/2$。所以可提取出光谱项 ${}^4\text{F}$。

最后得到的 ${\text{d}}^3$组态的所有的光谱项为：${}^2\text{H},{}^2\text{G},{}^4\text{F},{}^2\text{F},{}^2\text{D}(2),{}^4\text{P},{}^2\text{P}$

以上方法适用于任何同科电子组态光谱项的求算。而对于存在不同壳层的组态（例如 ${\text{p}}^2{\text{d}}^2$），只需要先分别求得p轨道的电子以及d轨道的电子的组合，再将不同角量子数的组合再一次组合即可。以 ${\text{p}}^2{\text{d}}^2$组态为例，此时总的微观状态数为 $\left(\begin{array}{c}6\\ 2\end{array}\right)\times \left(\begin{array}{c}10\\ 2\end{array}\right)=15\times 45=675$。这一方法说不上很高效，但思路很简单。之后生成表格的步骤则是完全一样的。

代码的思路

下面主要介绍代码的思路。

首先以$d$轨道的同科电子组态为例。

d轨道共有10个自旋轨道，所以声明了两个含有10个元素的数组分别储存各自旋轨道的磁量子数和自旋磁量子数。

电子数是由用户输入的，然后依次列举所有的自旋轨道的组合并计算 $M_L$和 $M_S$并分别储存在两个数组中。这里需要注意，由于电子数并非事先写在程序中，所以列举组合的部分无法直接使用嵌套的循环来做到（订正：实际上是可以的）。这里使用的是一个利用递归的子程序来实现的。

然后统计 $M_L$和 $M_S$的取值各有多少种，并生成两个数组分别储存这些值（按由大到小的顺序依次储存）。

例如：120种组合的 $M_L$依次为 $(5,3,2,3,-1,5,4,-2,...)$，而之后的那个数组为 $(5,4,3,2,...,-4,-5)$ 这11个值。

我们将前一个数组中的120个值与后一个数组进行比较，记录各个值出现的次数，便能够生成之前那个表中的数据。

对于具有不同角量子数的轨道的组态来说，则是分别将各个轨道上的组合再一次组合一次。 运行示例：

关于直接输出光谱项的功能的实现

由于直接对输出的表格进行操作很麻烦，而且也不必要（因为对整个表格操作需要的循环实现困难，而且表无论是行还是列都是对称的）。所以为了实现该功能，我首先取原有的表格的左上部分单独存为一个如图所示的二维数组。

之后检查第一行各列的数字 $n$，若为零，则跳过；若非零，则根据其对应的总角量子数 $L$和总自旋角量子数 $S$得到其光谱项（若不为1，输出的光谱项后会有类似<n>的标记，表明该光谱项的数目为 $n$），之后的各行与各列都减去 $n$。一行结束后，进入下一行，重复以上的步骤。（没看明白的话，可以按照第一节的例子跟着手算一下）

最终得到的结果是

对于多个壳层的情况（例如 $p^2{d}^2$），则是分别计算各壳层的所有组合，再按壳层进一步组合获得所有可能的情况。如果理解了前面的步骤，这一步并不难理解。之后确定光谱项的方法是完全一样的。

多个相同角动量相同的壳层也是可以计算的，如

参考文献

1. Journal of Chemical Education, 52(2), 1975:87-89
2. 大学化学, 29(2), 2014:44-46