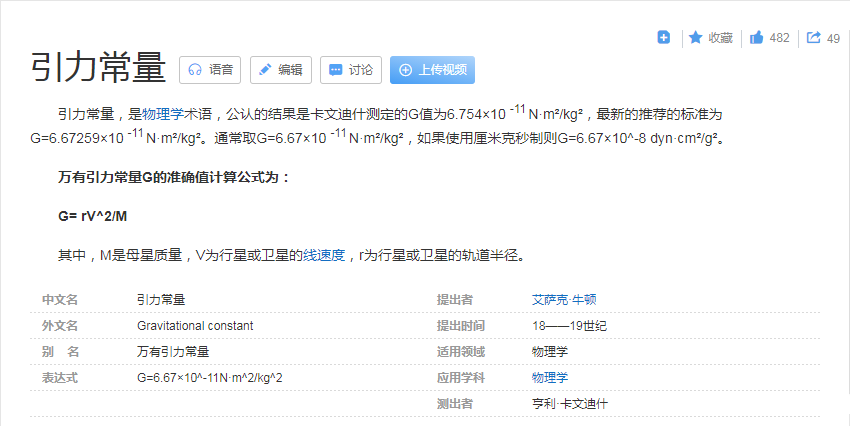
三、由轨道参数计算关机点参数
中学物理就讲过,卫星的轨道形状是一个椭圆。地球在椭圆的一个焦点上,而椭圆的参数包括半长轴a、偏心率e。

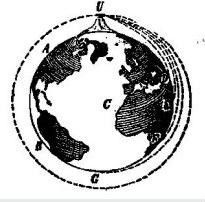
在研究轨道问题时,常常在极坐标系下进行,如下图所示。

图中,$p$为近地点,$a$为远地点。已知轨道近地点到地心的距离$r_a$,远地点到地心的距离$r_p$,近地点的位置$p$,关机点与地心连线与$op$的夹角为$f_k$。那么关机点参数可以用下面的公式进行计算。
关机点到地心的距离
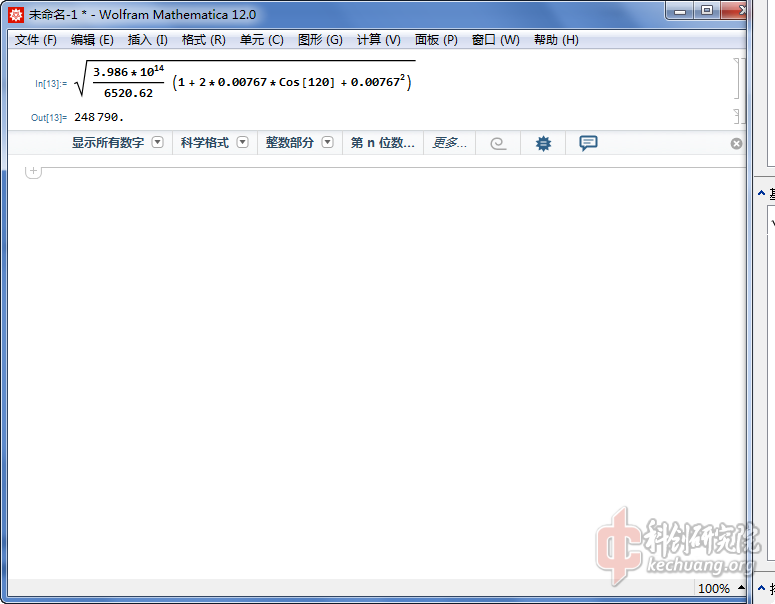
$$r_k=\frac{p}{1+e\cdot cosf}$$
关机点的速度大小
$$V_k=\sqrt{\frac{\mu }{p}(1+2\cdot e \cdot cosf+e^2))}$$
关机点弹道倾角为(弹道倾角:速度方向与当地水平面的夹角)
$$tan\Theta =\frac{e\cdot sinf}{1+e\cdot cosf}$$
其中,
$\mu$为地球引力常数,$\mu=3.986\times 10^{14}$,
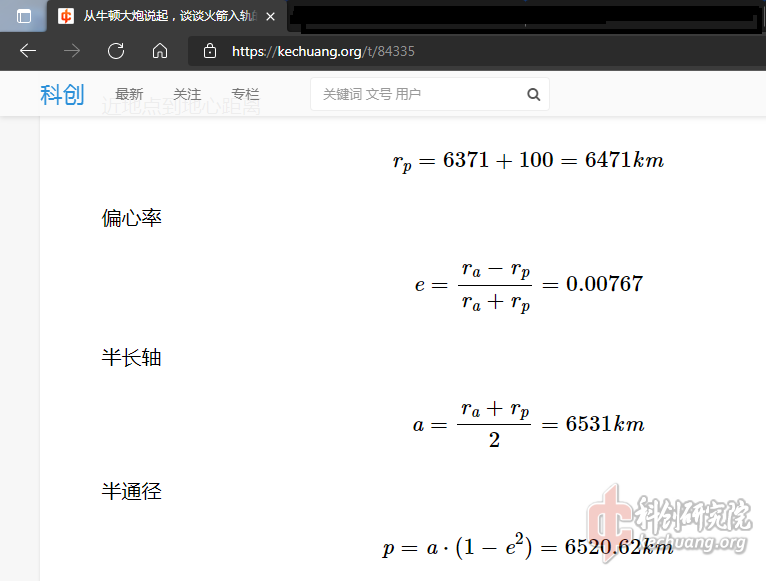
$e$为椭圆轨道偏心率,$e=\frac{r_a-r_p}{r_a+r_p}$,
$a$为椭圆半长轴,$a=\frac{r_a+r_p}{2}$,
$p$为椭圆半通径,$p=a\cdot (1-e^2)$。
此外要想成为地球卫星,还有一些附加条件。
(1)关机点速度应小于第二宇宙速度,因为大于第二宇宙速度的话就飞离地球了。
(2)弹道倾角应在0~90(不包括90度)度之间,$\Theta=90^{\circ}$垂直向上发射火箭一定会落下来。
(3)椭圆轨道不应与地面有交点。因为砸到人不好。














200字以内,仅用于支线交流,主线讨论请采用回复功能。